Yo-yo: un piccolo laboratorio di fisica

Fig. 1

Ragazzo che gioca con yo-yo di terracotta

Kylix dell’Attica, ca. 440 a.C.

Antikensammlung Berlin (F 2549)

Chi non ha mai giocato con uno yo-yo?

Lo yo-yo è un giocattolo, ma anche un attrezzo di giocoleria; consiste in due coppette unite da un asse centrale o da un cuscinetto a sfera in metallo nei modelli più moderni. L’oggetto è completato da un cordino di cotone o di nylon e poliestere, avvolto attorno all’asse di rotazione.

Il gioco consiste nel lasciar cadere il corpo rigido, tenendo fermo un capo del cordino; sotto l’azione della forza di gravità, agente sul centro di massa dello yo-yo, le coppette scendono e accumulano energia cinetica rotazionale e energia cinetica di traslazione.

Cosa accade quando le coppette sono arrivate nel punto più basso, ovvero quando il filo è completamente svolto? La particolarità dello yo-yo è che l’energia cinetica rotazionale è più grande di quella traslazionale di un paio di ordini di grandezza (100 volte maggiore)!

Negli yo-yo classici, come quelli di una volta, la corda è unita all’asse con un semplice cappio e l’asse ha la possibilità di ruotare all’interno di questo cappio.

In termini pratici tutto ciò significa che, quando i dischi sono arrivati al fondo della corda, se non si applicano altre forze, essi continuano a ruotare senza modificare la loro posizione spaziale e quindi non risalgono lungo il filo.

Per fare risalire lo yo-yo il giocatore deve dare uno ”strappo” alla funicella, aumentando l’attrito tra la stessa e l’asse, consentendo alla corda di riavvolgersi.

Uno yo-yo moderno non necessita più dello strappo alla funicella, perché il cordino è legato saldamente all’asse e quindi il corpo, dovendo ruotare, deve avvolgere o svolgere il cordino. In questo caso, una volta raggiunto il fondo, lo yo-yo comincerà sicuramente la risalita. 

Se non ci fossero attriti i due dischi sarebbero in grado di ritornare sempre alla stessa altezza di partenza, ma nella realtà, dopo ogni ciclo di discesa e salita, raggiungono altezze via via minori. 

Diamo una descrizione più analitica al fenomeno, studiando il bilancio energetico. 

Dal punto di vista fisico l’energia potenziale iniziale dello yo-yo viene convertita in energia cinetica del centro di massa ed energia cinetica di rotazione e la maggior parte dell’energia, al pari di un giroscopio, è sfruttata per la rotazione.

Per la conservazione dell’energia meccanica possiamo scrivere

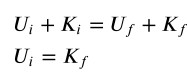
relazione che diventa:

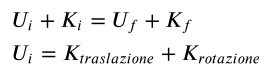
Esplicitando le espressioni dei vari tipi di energia,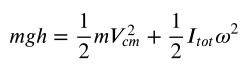

con 

Se consideriamo uno yo-yo vecchio modello, con la corda legata non troppo saldamente all’asse, arrivato al fondo della discesa prosegue la rotazione, che cesserà dopo poco. Di fatto l’energia rotazionale sarà dissipata e non ci sarà alcun cammino di risalita.

In figura è rappresentato il sistema di riferimento e le forze agenti sullo yo-yo. Trascurando gli attriti e la resistenza dell’aria, si può descrivere il moto di discesa con le relazioni:

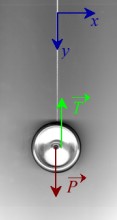
Fig. 2

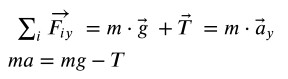
Quando lo yo-yo raggiunge il fondo si ha

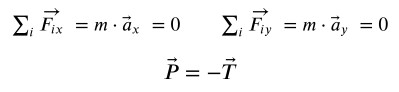
Indicando  la forza di attrito con

possiamo scrivere il secondo principio della dinamica rotazionale come

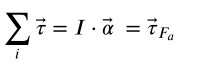
Quando il corpo è fermo al fondo della discesa

A questo punto è necessario lo “strappo” verso l’alto che produce un cospicuo incremento dell’attrito tra filo e asse ed un momentaneo aumento della tensione, ciò implica come conseguenza che lo yo-yo inizi la sua scalata.

Indichiamo con 

la forza esterna impulsiva  applicata con lo strappo verso l’alto e con

il lavoro svolto da questa forza.

Nell’istante t si ha che

Mentre lo yo-yo continua a risalire la corda, l’energia cinetica dello yo-yo è convertita in energia potenziale gravitazionale corrispondente alla crescente altezza della posizione del centro di massa. 

Per questa ragione, nel corso della salita, il momento angolare dello yo-yo e la sua rotazione diminuiscono costantemente. Questo è, naturalmente, il processo opposto alla discesa dello yo-yo.

Durante la risalita vale la seguente relazione

Affrontiamo adesso un esercizio numerico.

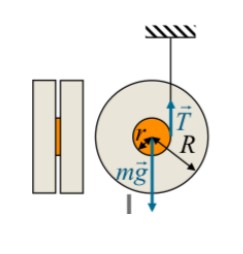
Fig. 3

Uno yo-yo è costituito da un cilindro omogeneo scanalato, di raggio R = 7 cm e massa m = 100 g, sulla cui gola, di raggio r, è avvolto uno spago, fissato con l’altra estremità al soffitto.

Calcolare l’accelerazione dello yo-yo e la tensione del filo T.

Scriviamo le equazioni della dinamica (bilancio forze e momenti torcenti):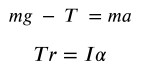

Ricordando che

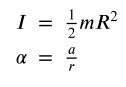
scriviamo:

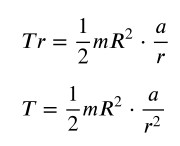
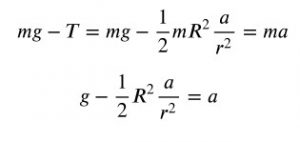
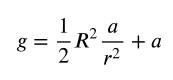
Dall’ultima relazione ricaviamo la formula dell’accelerazione di traslazione dello yo-yo:

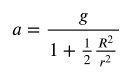
Introducendo i dati del problema otteniamo

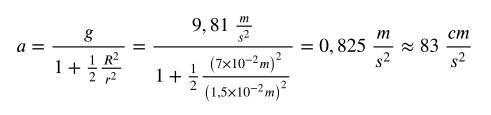
Interessante notare come nella formula dell’accelerazione non compaia la massa, ma compaiano solo le caratteristiche geometriche del sistema.

Per calcolare la tensione del filo dalla prima relazione scritta ricaviamo T:

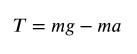
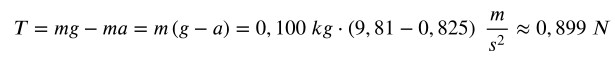
Terminiamo ora con un po’ di storia! Quando è nato il primo yo-yo?

Si pensa che lo yo-yo abbia avuto origine in Cina e che, molto probabilmente, da lì sia arrivato in Grecia dove si trovano le prime tracce storiche in documenti del 500 a.C. Il giocattolo poteva essere fatto di terracotta dipinta, di legno, di metallo.

Fig. 4

Dama che gioca con lo yo-yo 1791

In Europa lo yo-yo arrivò nel XVIII secolo, apparve in Inghilterra come una curiosità orientale, ma divenne popolare con il nome di bandilor. Secondo un articolo del “Journal de Luxes” del dicembre 1791, lo yo-yo arrivò a Parigi nell’ottobre dello stesso anno come “joujou de nomadie”.

Una stampa dell’anno 1792 mostra un gruppo di soldati giocatori di yo-yo in cui uno di loro gioca addirittura con due yo-yo contemporaneamente.

Nel 1795, in Francia, durante il regno del Direttorio, un gran numero di aristocratici si rifugiarono in Germania con i loro preziosi yo-yo realizzati in vetro e avorio; forse è questo il motivo per cui lo yo-yo era chiamato con i nomi di ”emigrette” e “coblentz”.

Il primo brevetto ufficiale, però, arrivò nel 1866 dal governo americano, ma lo yo-yo rimase nell’anonimato fino a che Pedro Flores aprì la Yo-Yo Manufacturing Company a Santa Barbara in California.

L’azienda fu successivamente acquistata da un imprenditore di nome Donald Duncan che intravide le potenzialità di questo gioco.                 

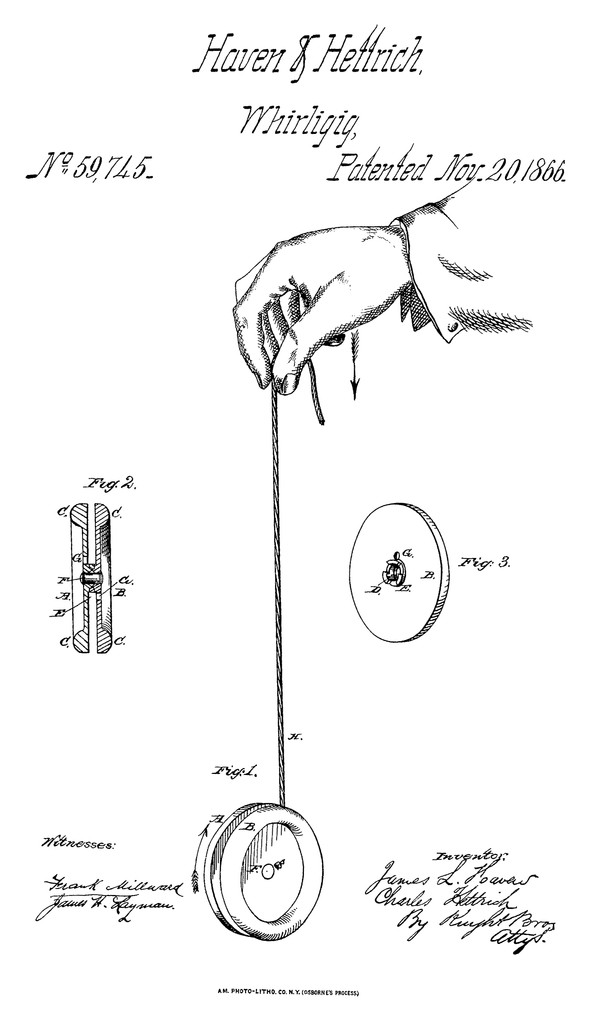
Fig. 5

Illustrazione dal brevetto americano del 1866

Da allora lo yo-yo ha fatto tanta strada, si è evoluto grazie a molte innovazioni tecnologiche come i cuscinetti a sfera, l’asse “frizionato”, la scelta dei materiali.

L’antico gioco è diventato strumento per fare spettacolari esibizioni, in cui si susseguono trick sempre più complessi, termine con cui si intendono le figure che si possono eseguire mentre lo yo-yo è in sleeper.

Lo sleeper è quella fase in cui lo yo-yo arrivato in fondo alla corda, continua a girare sul suo asse e continuerà a farlo sempre di più, via via che la tecnica di lancio migliorerà.

E poi? La gloria!

Dopo aver imparato tutto questo vi attendono il freestyle e la partecipazione ai campionati nazionali e internazionali!