L’ipnotica oscillazione del pendolo!

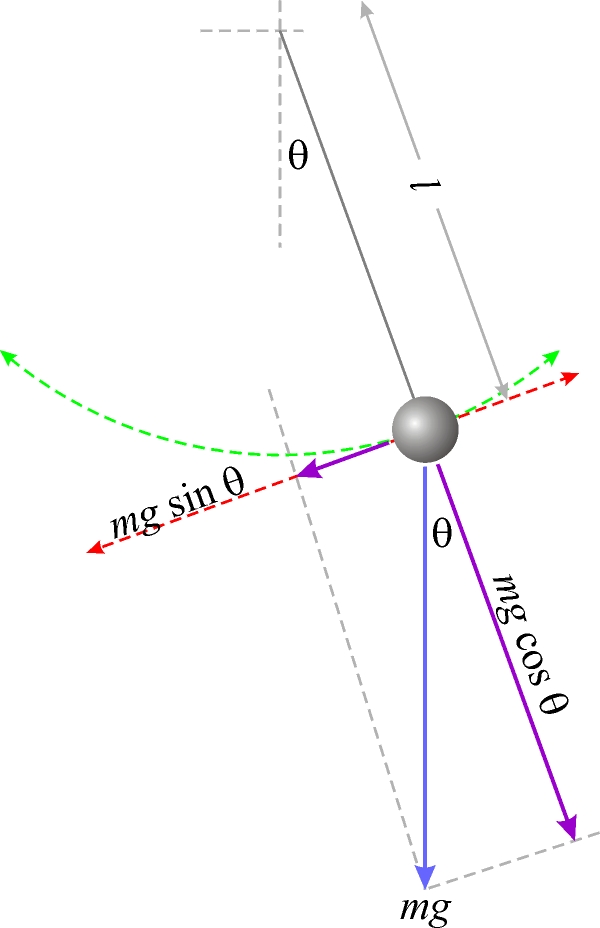
Fig. 1

Che cos’è un pendolo?

Il pendolo semplice è un sistema fisico costituito da un filo inestensibile e da una massa puntiforme (m) fissata alla sua estremità e soggetta all’attrazione gravitazionale, che supponiamo uniforme nello spazio e costante nel tempo.

Si tratta di un sistema banale, reso celebre da Galileo Galilei che, con il suo impegno sperimentale e teorico, descrisse correttamente la principale proprietà di un pendolo, ovvero l’isocronismo delle oscillazioni.

Cosa vuol dire isocronismo? Il termine significa che il periodo di un’oscillazione completa si mantiene costante nel tempo e, per piccole oscillazioni sotto i 5°, è indipendente dall’ampiezza dell’angolo. Ricordiamo, inoltre, che il periodo è il tempo impiegato dal pendolo per andare da un estremo all’altro e ritornare al punto di partenza.

In una situazione di piccole oscillazioni il pendolo si comporta come un oscillatore armonico con periodo:

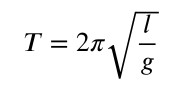
Osservando la formula si vede che T non dipende né dall’ampiezza delle oscillazioni (attenzione: devono comunque rimanere “piccole”!), né dalla massa appesa al pendolo, ma solo dal rapporto tra la lunghezza l del filo del pendolo e l’accelerazione di gravità g.

Quanto dura la danza del pendolo?

Teoricamente ha durata infinita! Ma esiste l’attrito viscoso dell’aria che smorza rapidamente le oscillazioni; infatti la resistenza del fluido dissipa energia meccanica non consentendo più l’eterna trasformazione dell’energia cinetica in energia potenziale gravitazionale e viceversa.

Qual è la condizione perché ci sia uno smorzamento dell’oscillazione?

Ogni volta che è presente una forza di attrito dinamico causata da  fattori vari, come gli attriti meccanici fra l’oggetto oscillante e il suo supporto fisso, oppure attriti dovuti alla resistenza del mezzo in cui l’oggetto oscilla, si osserva lo smorzamento dell’oscillazione.

Sperimentalmente si verifica che la forza di smorzamento è una forza variabile nel tempo e, con buona approssimazione, proporzionale alla velocità dell’oggetto oscillante; ovviamente la forza smorzante agisce in verso opposto al moto.

Il coefficiente 𝜼 dipende dalla viscosità del mezzo e quindi è legato all’intensità dell’attrito meccanico.

Come posso studiare la dinamica del moto?

É possibile scrivere l’equazione del moto in presenza di attrito inserendo anche la forza di smorzamento nella seconda legge della dinamica:

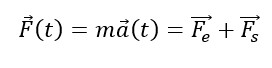
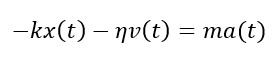
che è l’equazione del moto di un oscillatore armonico smorzato, in cui l’ampiezza dell’oscillazione x(t) diminuisce al trascorrere del tempo, mentre il periodo si mantiene sostanzialmente costante.

Facciamo un bel salto di qualità nel nostro modello matematico?

Le grandezze accelerazione e velocità possono essere espresse in termini di derivate: la velocità è la derivata prima dello spazio in funzione del tempo e l’accelerazione, essendo la derivata della velocità rispetto al tempo, può essere scritta come la derivata seconda dello spazio in funzione del tempo.

L’equazione del moto, dopo aver riordinato i termini, diventa:

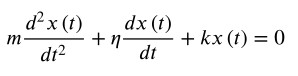
Se dividiamo tutti i termini per m si ottiene l’equazione differenziale per il moto armonico smorzato, un’equazione differenziale lineare omogenea del secondo ordine, a coefficienti costanti.

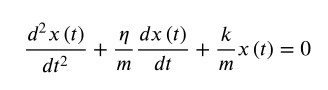
Questo tipo di equazione ha una soluzione contenente un fattore esponenziale… tranquilli omettiamo il procedimento per la risoluzione, e scriviamo subito la legge oraria del moto armonico smorzato:

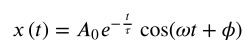
All’esponente compare il tempo con un meno davanti; ciò significa che al trascorrere del tempo il valore dell’ampiezza di oscillazione diminuisce.

Il termine 𝜏 è la costante di tempo o tempo caratteristico, che si definisce come il tempo necessario affinché l’ampiezza iniziale si riduca di un fattore 1/e. La costante di tempo è uguale a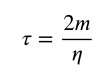

La pulsazione 𝜔 è data dalla seguente relazione: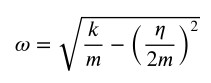

Rispetto al moto armonico non smorzato la pulsazione del moto armonico smorzato assume valori più piccoli e ciò implica che il periodo di oscillazione sia maggiore; la presenza dell’attrito rende il moto più lento e allunga i tempi di oscillazione.

Esiste un caso limite in cui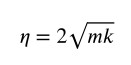

e la pulsazione 𝜔 si annulla. Cosa significa? Che non ci sono più oscillazioni, l’ampiezza decresce in modo esponenziale, ovvero l’attrito è tale da rallentare la massa m dalla posizione iniziale alla posizione di equilibrio, senza che possa oltrepassarla, impedendo l’oscillazione.

Un po’ di grafici…

A questo punto vediamo il grafico di variazione dell’ampiezza di oscillazione di un oscillatore armonico smorzato a seconda del tipo di smorzamento.

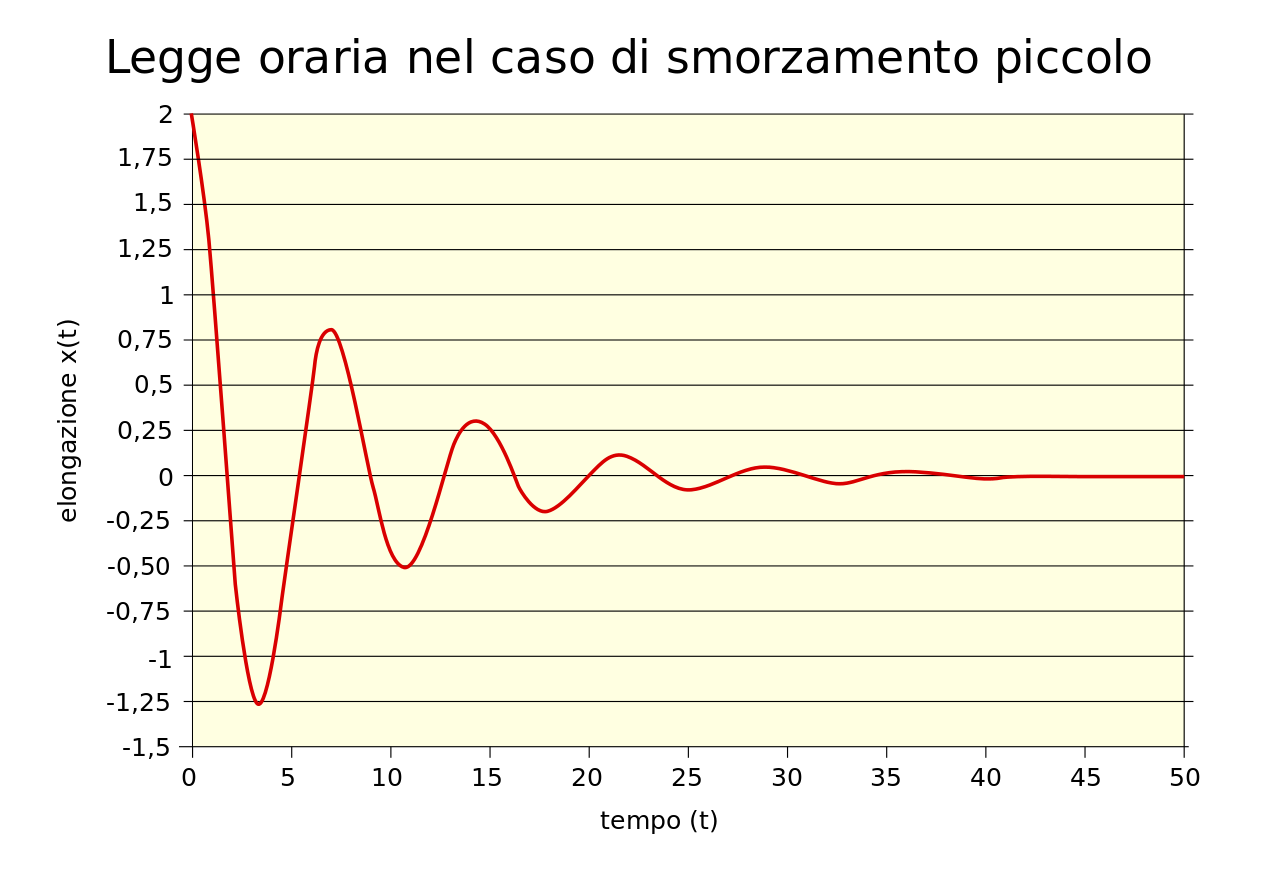
Fig. 2

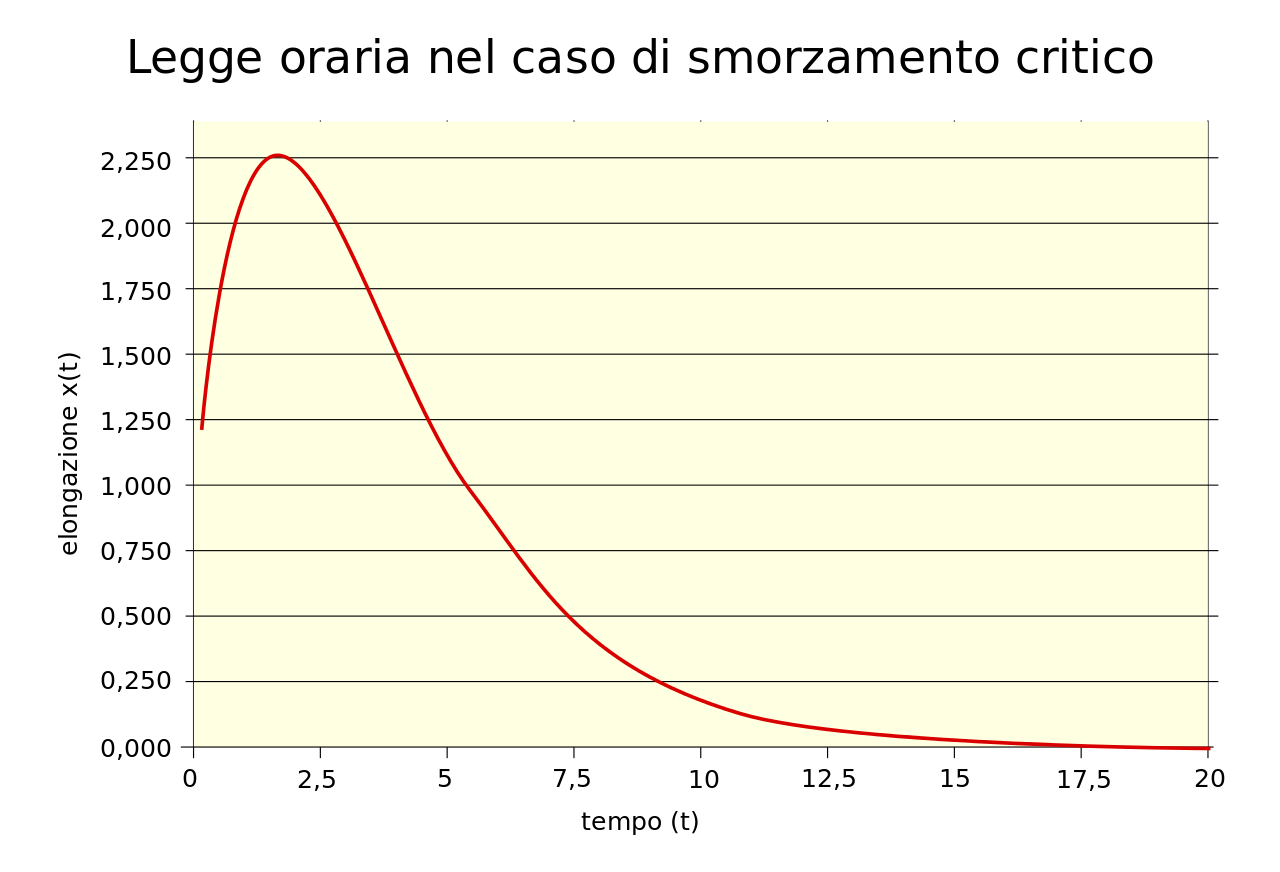
Fig. 3

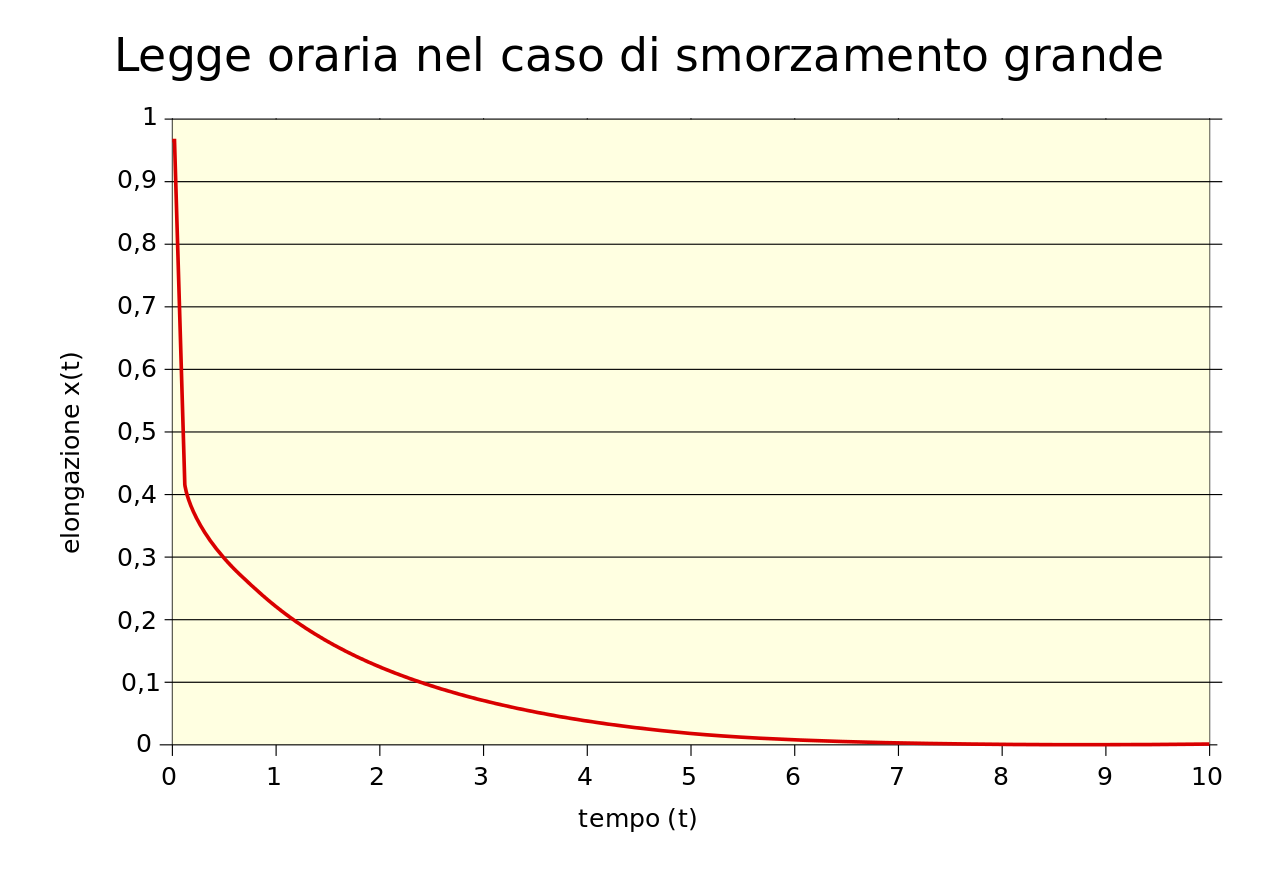
Fig. 4

E da un punto di vista energetico?

Nel caso di un oscillatore armonico ideale l’energia meccanica si conserva ed è data dalla seguente relazione

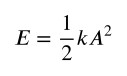
Ma se agiscono le forze di attrito il bilancio energetico si modifica: l’energia meccanica non si conserva, ma si riduce progressivamente, considerato che l’ampiezza di oscillazione non è costante. Cosa accade all’energia meccanica?

L’energia meccanica “scomparsa” si è trasformata per dissipazione in altre forme, come ad esempio in calore.

L’espressione dell’energia meccanica nel caso dell’oscillatore armonico smorzato è data dalla legge:

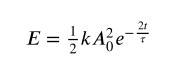
in cui l’ampiezza A decresce al passare del tempo e l’energia meccanica diminuisce nel tempo due volte più rapidamente di quanto decresca l’ampiezza di oscillazione.

Si può fornire una stima dell’intensità dello smorzamento non solo calcolando il tempo caratteristico 𝜏, ma determinando una quantità adimensionale che tiene conto del rapporto fra il valore assoluto dell’energia 𝜟E dissipata a causa degli attriti in un periodo di oscillazione e l’energia totale E a disposizione.

Questa quantità si chiama fattore di qualità o di merito ed è definita tramite la seguente relazione: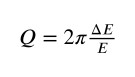

in cui   

è la frazione percentuale  di energia dissipata in un periodo; minore è la frazione percentuale di energia persa nel moto a causa degli attriti, più è alta la qualità Q dell’oscillatore.

Questo fattore di merito viene utilizzato, ad esempio, in ingegneria elettronica nello studio dei circuiti RLC.